One Key is kept private by the entity, and the other is made public available.
Crypto = Cipher
Hashing 雜湊(隨機) Symmetrics 對稱 Asymmetrics 非對稱
(Private Key) (Public Key)
/ \
/ \ / \ / \
/ \ / \ / \
SHA MD5 / \ / \
Block 區塊鏈 Stream 串流 RSA Diffle-Hellman
/ | \ | \ (可用於不安全的加密通道的金鑰建立演算法)
/ | \ | \
DES AES BlowFish RC4 TKIP
Encryption = Encipherment
-
Hash: 雜湊提供 checksum ,為訊息摘要,由可變動長度之訊息產生,摘要比訊息簡短,摘要和訊息一起送給接收者。
-
Asym: 公開加密金鑰,擁有 2 把金鑰 public key & private key,,傳送者使用公開金鑰加密文件後,傳送予接收者,接收者則使用私密金鑰解開加密文件。
-
Sym: 秘密金鑰,將訊息安全地於兩個實體間 (傳送者與接收者) 往返。
Status Quo in case using Security Schematics:
-
網站要求使用者登入系統時提供身分證明。(Auth & Exchange Authentication)
-
使用者登入系統狀態在數分鐘內,伺服器強迫使用者登出。(setTimeout to avoid Middleman)
-
某機構拒絕透過電子郵件寄送機密性資訊予使用者,要求使用者提供身分證明。(Auth & Exchange Authentication)
-
銀行需要客戶的簽章,方才提供提款服務。(Digital Signature)
-
Secuity Attacks
-
Symmetrics Encryption Algorithm
-
Encryption Arithmetics : Algebra
-
Symmetrics Encryption & Decryption
-
Traditonal Encryption & Decryption
-
Modern Encryption & Decryption
-
Symmetrics Encryption Algorithm for Stream & Block
-
Asymmetric Encryption Arithmetics : Function for congruence
-
Asymmetrics Encryption & Decryption(RSA, ECC)
-
Digital Signature for Integrity (RSA, ECC)
-
Hashing Algorithm in Exchange Authentication (omit)
ITU-T
https://www.itu.int/en/ITU-T/Pages/default.aspx
Security Attacks
Passive Active
(middle man)
snooping modification DDoS
throughput masquerading
replay
repudiation
Confidentiality Integrity Availability
機密 完整 可用
(1) 防衛惡意行為 (1) 系統中斷影響完整性 儲存資訊的地方能讓被授權者存取
(2) 隱藏敏感性資訊 (2) 經常需要更動且須經授權的資訊
Authentication
身分確認 資料完整能防止遭竄改抑或是重送 攸關存取控制
藉由來源證明與傳送證明佐證不可否認性
Encrypt Digital Certificate ACL
Security Mechanism
|----- Encrpt
|-------------Integrity
|----------------------- Digital Signature
|------------------------------------------- Authentication Exchange
|----------------------------------------------------------------------Thoughput Monitor
|-----------------------------------------------------------------------------------Router Control
|------------------------------------------------------------------------------------------------ Notarization
|-------------------------------------------------------------------------------------------------------------- ACL
modular arithmetics
@param(a, r)
a = q * n + r
|
|
V
@mod is modulo operator
@n is modulus
@r is residue
a mod n = r or a % n = r
@set og least residues modulo n
Z = { }
congruence 同餘
It means equality in Cipher.
2 mod 10 = 2
12 mod 10 = 2
22 mod 2 = 2
residue class
x = a (mod n)
for n in range(0, 3):
[0] = { xSetmodN }
[1] = { xSetmodN }
[2] = { xSetmodN }
apply field of modulo arithmetics
生活中會使用模數運算,例如 12 點由 0 替代,第二次循環時,由 am 轉成 pm。
Matrix & Linear Algebra
-
row matrix, 行矩陣
瘦長的矩陣 -
col matrix, 列矩陣
橫向的矩陣 -
square matrix, 方矩陣
方形的矩陣,使用行列式 det(A), det 即 determinant -
residue matrix, 餘數矩陣
整數矩陣後還須運行一次模數運算
Algebra Stucture
G R F
Group Ring Field
群 環 體
/ | | | \ | ||
/ | | | \ R=<{}, . , 2nd ops> a Ring without the ability of existence of inverse
/ | | | \ the 2nd ops matches the ability of distributivity
commutative| | | existence of inverse
closure | existence of id
associative
-
commutative, 交換性
-
closue, 分配性
-
associative, 可結合姓
-
id, 存在單位元素
-
inverse, 存在反元素
-
disbutivity, 可分配性
-
{}, a Group
-
. , the operator
-
2nd ops
UML
sender receiver
plaintext ----------------------------- plaintext
(Encrpto) secure tunnel (Decrpto)
encrpted file ----------------------------- encrpted file
Kerckoff's Principle
根據此原則,須假設解密或攔截密文的敵人知道加解密演算法,密鑰為唯一抵抗力,基於金鑰範圍 key domain 非常廣,猜測金鑰相當困難,所以無須將演算法隱藏起來。
cryptanalysis, 破密分析是科學也是藝術:
Analysis Atack
Brute-force Attack(exhausive-key-search), statistical attack, pattern attack
|
-------------------------------------------
| | | |
ciphertext-only | | |
| known-plaintext | |
| | chosen-plaintext |
v | chosen-ciphertext
最常發生但最難破解 | |
V |
已知明文是最容易執行的攻擊 |
發送者傳送加密文件後又傳送明文 |
攻擊者方便比照兩文件做破解分析 |
|
v
攻擊者選擇明/密文對
-
substitution cipher, 取代加密法
用字母取代另一個的加密法,傳統上取代加密法有單字母以及多字母的選擇。
單字母 >
-
加法
-
乘法
-
仿射
多字母 >
-
自動金鑰
-
playfair
-
vigenere
-
hill
-
單次密碼本
-
迴轉加密
-
迷團機
-
-
transposition cipher, 換位加密法
重新安排符號順序的加密法,目前的選擇有: (1)無金鑰的換位加密、(2)有金鑰的換位加密、(3)雙位換位加密。
傳統的加密基礎是字元 char 導向,而現代加密技術則以位元 bit 作為導向。 如此一來,便不僅止於家密文檔,亦可加密圖檔或是音訊抑或是視訊等資料 ! 將如上類型的資料轉換成為一連串位元 Bit -> Byte -> Buffer -> Streaming,最後變成加密的串流是現代很常見的加密行為。
char -> bit 轉型的優勢,使得文字被位元替代後,每一字元會變成 8 or 16 bits 取代,則符號數量變成 8 or 16 倍,符號的量增加,安全性也增加。
modern Stream Cipher (RC4)
串流一次以一字元或是一位元對其串流加密,有明文串流P (pipeline)、密文串流C (ciphered stream)、金鑰串流K (key)。
現在串流加密法中,明文串流中的每個 r 位元字組使用金鑰串流中的一個 r 位元自組進行加密,以便產生密文串流中相對應的 r 位元字組。
kn kn
. .
. .
. .
k1 k1
pn...p1 ---> Encrpt --- cn...c1 -- > Decrpt ---> pn...p1
modern Block Cipher (DES/ AES)
加解一個 n 位元的明文區塊或解密一個 n 位元的密文區塊
倘若訊息小於 n 位元,須加入填塞位元,使其成為 n 位元區塊;
趟若訊息大於 n 位元,則分割成數個 n 位元區塊,
一般 n = 64 or 128 or 256 or 512。
Pln int ext ----- > Enc rpt fil
n 位元明文 --- K 位元金鑰加密 ---> n 位元密文 --- K 位元金鑰解密 ---> 明文
Combination of Stream of Blocks
明文區塊是獨立加密的,但利用 key 串流將區塊和區塊加密成為整個訊息。 就宏觀角度而言,整條訊息是串流加密,但就細微角度反觀,則單一區塊使用區塊加密。
- Discrete Math
離散數學即非連續性數學,通常討論整數不討論浮點數,相對微積分而言,微積分是連續性且可微,離散數學討論的對象包含:
0 or 1, bool
<> or [], set or arraylist
Graphics 擁有較為零散的結構,可以舉的例子例如 FB 好友關係
Algebra 擁有有系統的結構
非連續性的數值分析或計算,可算出可能的排列組合,應用範疇包含:
組合
集合
圖
網路流量
遞迴 (可計算執行多久)
- Galois Field = Finit Field
有限體與 RSA 有關,是包含有限個元素的體,與其他 field 一樣,有限體是進行加減乘除運算都有定義且滿足特定規則的集合,最常應用在 p 為質數,整數對 p 取模。
+ | 0 1
--+----
0 | 0 1
1 | 1 0
+ | 0 1 A B
--+--------
0 | 0 1 A B
1 | 1 0 B A
A | A B 0 1
B | B A 1 0
- Prime Number
質數指除了 1 和能被其他自然數整除的數,質數的相反是合成數。歐基里德發現了無限多個質數存在的定理。
- RSA
RSA_keys_generator(){
p is prime number
q is prime number
p != q
n <- p * q
Φ(n) <- (p -1) * (q - 1)
e is in range that 1 < e < Φ(n)
d <- e^1 mod Φ(n) # Φ ?
Pub_key <- (e, n)
Priv_key <- d
return Pub_key, Priv_key
}
- Elliptic Curve Crypto, 橢圓曲線
相對於 RSA 這樣有代價(長度過長)的金鑰密碼系統,替代方案則為橢圓曲線。
p is modulo
(x, y) is the point on the curve
ECC_points_generator(p, x, y){
q <- 0
while(q<p){
w <---(q*q*q + x*q +y) mod p
if(w is a perfect squre in zigma_p) then output (q, sqrt(w)) (q, - sqrt(w))
q <- q +1
}
}
- Rabin
基於計算模合數平方根困難性問題的公鑰密碼演算法
(omit)
- ElGamal
diff-hellman 的非對稱版本,ElGamal 可定義在任何循環群 G 上。它的安全性取決於 G 上的離散對數難題。
(omit)
Definition
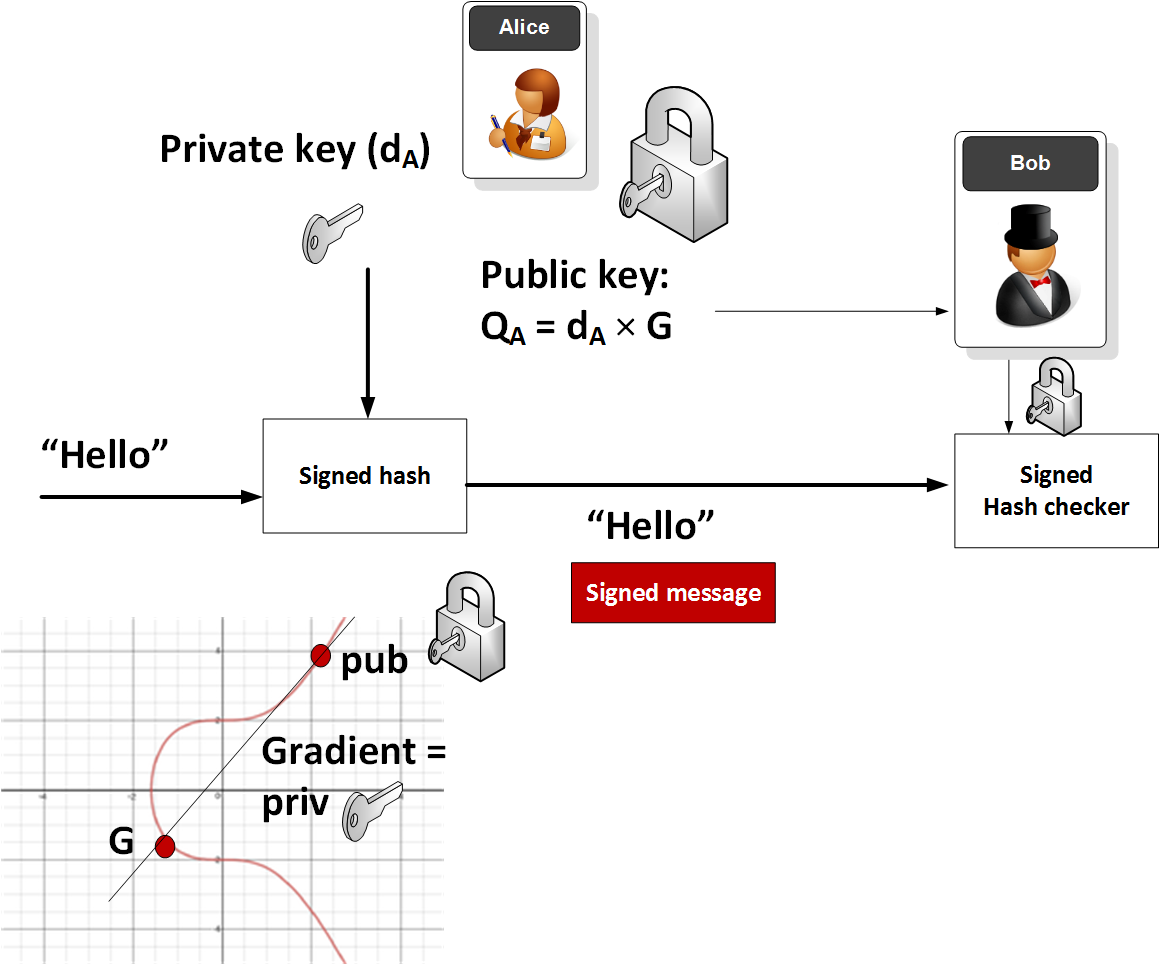
數位簽章的加解密演算法使用 RSA 抑或 ECC,然而公私鑰的腳色在數位簽章與一般加解密 文件的腳色相反。 在數位簽章實務中,私鑰是傳送者的,而非接收者的,傳送者使用自己的私鑰簽署文件, 而接收者使用傳送者的公鑰驗證文件 Authentication,Private Key 在此好比 Signature 正本, 而 Public Key 好比 Signature 副本。
UML
(to be continued...)